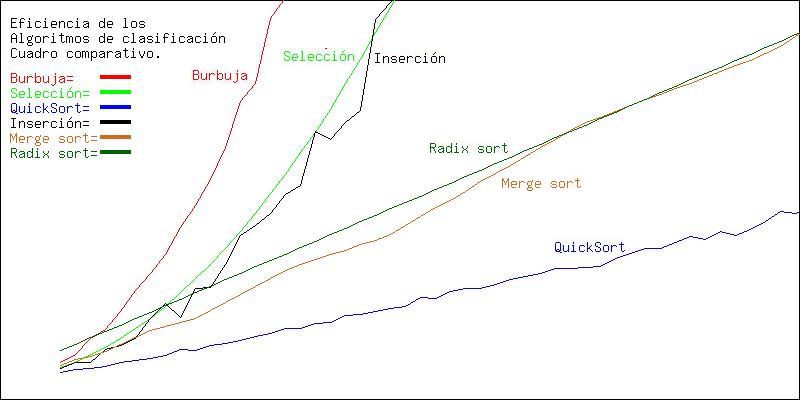
Determinante de una matriz, usando la reducción de Gauss.
Teoría: Estructuras. Temas de estudio. Menu Ecuación Temporal ->Algoritmos de orden cúbico
Orden de la matriz 

?
Clave 

Complejidad para el cálculo de:
i=N
∑ i !  =  Ο(n2)
i=1

 Ecuación temporal = 2+( 2(N( N + 1 ) ) ) + 7N

N =
Volver.
Transformar una matriz a su escalonada / Calcular el rango de una matriz
Orden de la matriz 
Filas:
Columnas:

?
Volver.
Complejidad del método de clasificación por   Burbuja. Ο(n2)
Teoría: Estructuras. Temas de estudio. Menú Ecuación Temporal -> Métodos de clasificación

Análisis del peor Caso. 
for(i=0;i < N-1; i++) {
	for(j=i+1; j < N; j++) {
		if(a[i] > a[j]) {
			temp=a[i];
			a[i]=a[j];
			a[j]=temp;
		}
	}
}
N 
?
?


 Ecuación temporal peor caso 6N2 - 3

 Ecuación temporal mejor caso (5N2 + 7N - 6) / 2

 Ecuación temporal caso promedio (17N2 + 7N - 12) / 4

N =
Mejor caso Caso medio

Volver.
Complejidad del método de clasificación por   Selección. Ο(n2)
Teoría: Estructuras. Temas de estudio. Menú Ecuación Temporal -> Métodos de clasificación

 Ecuación temporal (Peor caso)= Ejercicio: favor calcularla.

N =


Volver.
Complejidad del método de clasificación por   Inserción. Ο(n2)
Teoría: Estructuras. Temas de estudio. Menú Ecuación Temporal -> Métodos de clasificación

 Ecuación temporal = 8( (N/2)(N + 1) - N) + 12(N - 1) + 4

N =

Volver.
Complejidad del método de clasificación por   Radix Sort Ο(n)
Teoría: Estructuras. Temas de estudio. Menú Ecuación Temporal -> Algoritmo Radix-Sort

N =


Volver.
Complejidad del método de clasificación por   Quicksort. Ο(N lg(N))
Teoría: Estructuras. Temas de estudio. Menú Ecuación Temporal -> Algoritmo Quick-Sort

 Ecuación temporal = 44 - 23 N + 13 N lg(N)

N =
Volver.
Complejidad del método de clasificación por   Merge Sort. Ο(N lg(N))
Teoría: Estructuras. Temas de estudio. Menú Ecuación Temporal -> Algoritmo Merge-Sort

 Ecuación temporal = 70 - 68N + 39 N lg(N)

N =
Volver.
Comparación métodos de clasificación



Volver.
Complejidad de de la busqueda binaria   Busqueda Binaria. Ο(lg(N))
Teoría: Estructuras. Temas de estudio. Menú Ecuación Temporal -> Busqueda Binaria

 Ecuación temporal = 7 + 10 lg(N)

Prueba a la función:
Se genera un arreglo de N posiciones
con numeros aleatorios. Luego se clasifican
ascendentemente y se busca el número 50 con
la rutina de busqueda binaria y se calculan las
operaciones elementales por fórmula
y por contador.
N =

Volver.
Calculadora para ayudar a determinar si existe cota Ο de:

Con ayuda de la calculadora encontrar un rango [ n0 , n1 ]
donde exista cota... n1 puede ser, teoricamente ∞
Para esta calculadora, debería ser un número pequeño.
g = Ο( f ) Existe cota, si se
cumple la desigualdad
g <= c * f
  n+10 = Ο(n2)   n+10 <= c * n2
  2lg n = Ο(lg n )2   2lg n <= c * (lg n)2
  √(lg n) = Ο(4lg n)   √(lg n) <= c * 4lg n
  lg n = √(n)   lg n <= c * √(n)
Calculadora para buscar n y c donde exista la cota
Valor n =
Constante c = para diferentes valores de n
Volver.
Calculadora para ayudar a probar una propiedad

Primera
Propiedad		 Ο( f ) = Ο( g ) =>
     f = Ο( g ) y g = Ο( f )
Funciones
ejemplo		 f = 3lg n y g = lg n
Reemplazando en la propiedad:
Prueba 3lg n = Ο( lg n ) ==>
     3lg n <= c * (lg n )
Prueba lg n = Ο( 3lg n ) ==>
     lg n <= c * ( 3lg n )
Calculadora para buscar n y c donde exista la cota
Valor n =
Constante c = para diferentes valores de n
Volver.
Calculadora para ayudar a probar una propiedad

Segunda
Propiedad		 f = Ο( g ) y g = Ο( h ) =>
     f = Ο( h )
Funciones
ejemplo		 f = 3lg n , g = lg n , h = √(n)
Reemplazando en la propiedad:
Prueba 3lg n = Ο( √(n) ) ==>
     3lg n <= c * √(n)
Calculadora para buscar n y c donde exista la cota
Valor n =
Constante c = para diferentes valores de n
Volver.
Calculadora para ayudar a probar una propiedad

Tercera
propiedad. 		f = Ο( g ) y f = Ο( h ) =>
     f = Ο( min( g, h ) )
Funciones
ejemplo		 f = lg n , g = n2 , h = n3
Reemplazando en la propiedad:
Prueba lg n = Ο( n2 ) y lg n = Ο( n3 ) ==>
     lg n <= c * n2
Calculadora para buscar n y c donde exista la cota
Valor n =
Constante c = para diferentes valores de n
Volver.
Calculadora para ayudar a probar una propiedad

Cuarta
Propiedad. 		f1 = Ο( g ) y f2 = Ο( h ) ==>
     f1 + f2 = Ο( max( g, h ) )
Funciones
ejemplo		 f1 = lg n , g = n2 , f2 = n lg n , h = n3
Reemplazando en la propiedad:
Prueba lg n = Ο( n2 ) y n lg n = Ο( n3 ) ==>
     ( lg n + n lg n ) <= c * n3
Calculadora para buscar n y c donde exista la cota
Valor n =
Constante c = para diferentes valores de n
Volver.
Calculadora para ayudar a probar una propiedad

Quinta
Propiedad. 		f1 = Ο( g ) y f2 = Ο( h ) ==>
     f1 * f2 = Ο( g * h ) )
Funciones
ejemplo		 f1 = lg n , g = n2 , f2 = n lg n , h = n3
Reemplazando en la propiedad:
Prueba lg n = Ο( n2 ) y n lg n = Ο( n3 ) ==>
     ( ( lg n ) * ( n lg n ) ) <= c * n5
Calculadora para buscar n y c donde exista la cota
Valor n =
Constante c = para diferentes valores de n
Volver.
Calculadora para ayudar a probar una propiedad

Sexta
Propiedad
lim
n->∞ 		(f / g) = k
Si k es 0 f = Ο( g ) y g ≠ Ο( f )
Si k ≠ 0 y k < ∞ Ο( f ) = Ο( g ) ( Mismo orden )
Funciones
ejemplo		 f = n2 y g = n3
Reemplazando en la propiedad:
Prueba 1.
lim
n->∞ 		( (n2) / (n3)) = 0
Lo que implica que : n2 <= c * ( n3 )
Calculadora para buscar n y c donde exista la cota
Valor n =
Constante c = para diferentes valores de n
Segundo ejemplo de la sexta propiedad

Funciones
ejemplo		 f = (lg n)3 y g = n(1/3)
Reemplazando en la propiedad:
Prueba 2.
lim
n->∞ 		( (lg n)3) / (n(1/3)) ≠ 0
Lo que implica que : (lg n)3 <= c * ( n(1/3) ) no siempre se cumple
Calculadora para buscar n y c donde exista la cota
Valor n =
Constante c = para diferentes valores de n
Volver.
Calculadora para ayudar a determinar si existe cota θ

Con ayuda de la calculadora encontrar un rango [ n0 , n1 ]
donde exista cota θ... n1 puede ser, teoricamente ∞
Para esta calculadora, debería ser un número pequeño.
g = θ( f ) Existe cota, si se
cumplen las siguientes desigualdades
g <= c * f y g >= d * f
para dos valores reales c y d mayores que 0.
  √n = θ(lg n)   √n <= c * lg n   y   √n >= d * lg n
Calculadora para buscar n,c y d donde exista la cota
Valor n =
Constante c = para diferentes valores de n
Constante d = para diferentes valores de n
Volver.
 Primera propiedad. Cota θ 

lim
n->∞ 		(f / g) = k
Si k > 0 entonces:
f = θ(g)
Funciones ejemplo f = (lg n)3 y g = n(1/3)
Reemplazando en la propiedad:
lim
n->∞ 		( (lg n)3) / (n(1/3)) ≠ 0
Lo que implica que :
(lg n)3 <= c * ( n(1/3) ) y
(lg n)3 >= d * ( n(1/3) )
Calculadora para buscar n,c y d donde exista la cota
Valor n =
Constante c = para diferentes valores de n
Constante d = para diferentes valores de n
Volver.
 Segunda propiedad. Cota θ 

Si f = θ(g) y g = θ(h)
entonces: f = θ(h)
Funciones
ejemplo		 f = 2n , g = 2n+1 y
h = n2
Aplicando la propiedad:
2n <= c * 2n+1 y 2n >= d * 2n+1
2n+1 <= c * n2 y 2n+1 >= d * n2
2n <= c * n2 y 2n >= d * n2
Calculadora para buscar n,c y d donde exista la cota
Valor n =
Constante c = para diferentes valores de n
Constante d = para diferentes valores de n
Volver.
 Tercera propiedad. Regla de la suma. Cota θ 

Si f1 = θ(g) y f2 = θ(h)
entonces: f1 + f2 = θ( max(g, h) )
Funciones
ejemplo		 f1 = 3 + ln(n) , g = ln(n)
f2 = 5 + ln(n) y h = 2 ln(n)
Note que h, crece más rapido que g
Aplicando la propiedad:
3 + ln(n) <= c * ln(n) y 3 + ln(n) >= d * ln(n)
5 + ln(n) <= c * 2 * ln(n) y 5 + ln(n) >= d * 2 * ln(n)
8 + 2 * ln(n) <= c * 2 * ln(n) y
        8 + 2 * ln(n) >= d * 2 * ln(n)
Calculadora para buscar n,c y d donde exista la cota
Valor n =
Constante c = para diferentes valores de n
Constante d = para diferentes valores de n
Volver.
 Cuarta propiedad. Regla del producto. Cota θ 

Si f1 = θ(g) y f2 = θ(h)
entonces: f1 * f2 = θ( g * h )
Funciones
ejemplo		 f1 = 3 + ln(n) , g = ln(n)
f2 = 5 + ln(n) y h = 2 ln(n)
15+8*ln(n)+(ln(n))2
2 * (ln(n))2
Aplicando la propiedad:
3 + ln(n) <= c * ln(n) y 3 + ln(n) >= d * ln(n)
5 + ln(n) <= c * 2 * ln(n) y 5 + ln(n) >= d * 2 * ln(n)
15 + 8 * ln(n) + (ln(n))2 <= c * 2 * (ln(n))2 y
        15 + 8 * ln(n) + (ln(n))2 >= d * 2 * (ln(n))2
Calculadora para buscar n,c y d donde exista la cota
Valor n =
Constante c = para diferentes valores de n
Constante d = para diferentes valores de n

Nota: Para solucionar las ecuaciones en recurrencia favor estudiar el capítulo 19 del texto "Estructuras de datos en C++.".
Volver.
Cambio de Monedas con Programación dinámica.
Teoría: Estructuras. Temas de estudio. Menú Ecuación Temporal -> El problema de las vueltas
si i == 1 y j < valori entonces c[i,j] es ∞
sino si i == 1 entonces c[i,j] = 1 + c[1, j-valor1]
sino si j < valori entonces c[i,j] = c[i-1, j ]
sino c[i,j]= mínimo (c[i-1, j], 1 + c[i, j-valori] )
Número de monedas Valor de las vueltas. (1->30)
?
Volver.
Ejemplo para encriptar con RSA, el caracter 't'
t = 116 // ascii de 't'
p = 23 // primo
q = 31 // primo
n = 29 // primo
fi = (p-1) * (q-1)
z = p * q
 
(n * s) % fi == 1
Calcule s con un ciclo desde n+1 hasta
encontrar un valor que satisfaga la
igualdad.
 
( t ^ n ) % z es el valor encriptado
 
Usando la propiedad:
 
(ab) % z = ( (a % z) * (b % z) ) % z
 
tenemos que:
 
El Arreglo a[] tiene un tamaño igual al número de bits de n
 
( t ^ 1) % z = 116 almacenarlo en a[0]
 
( t ^ 2) % z = ((( t ^ 1) % z)*(( t ^ 1) % z)) % z = 622 a[1]
 
( t ^ 4) % z = ((( t ^ 2) % z)*(( t ^ 2) % z)) % z = 438 a[2]
 
( t ^ 8) % z = ((( t ^ 4) % z)*(( t ^ 4) % z)) % z = 47 a[3]
 
( t ^ 16) % z = ((( t ^ 8) % z)*(( t ^ 8) % z)) % z = 70 a[4]
 
y asi sucesivamente hasta analizar todos los bits de n (1 1 1 0 1)
 
Para el caso particular
los valores del arreglo a[] son:
 0 1 2 3 4
1166224384770
(t^1)%z(t^2)%z(t^4)%z(t^8)%z(t^16)%z
 
Como n en binario es:
 
1 1 1 0 1
4 3 2 1 0
Cada bit prendido corresponde a una posición del arreglo a[]
bit 0(a[0]), (bit 1 esta apagado), bit 2(a[2]), bit 3(a[3]), bit 4(a[4])
 
entonces
(t ^ 29) % z se calcula así:
 
(t ^ 5) % z es ( ((t ^ 1) % z) * ((t ^ 4) % z) % z) = 185 (a[0] y a[2])
 
(t ^ 13) % z es ( ((t ^ 5) % z) * ((t ^ 8) % z) ) % z = 139 (a[3])
 
(t ^ 29) % z es ( ((t ^ 13) % z) * ((t ^ 16) % z) % z = 461 (a[4])
 
Ejecutando las operaciones tenemos:
 
(116 * 438) % z = 185
(185 * 47) % z = 139
(139 * 70) % z = 461
 
De manera que el caracter
t encriptado es 461.
 
Para acceder a cada bit de n, lo podemos hacer con este ciclo:
 
k = 0;
while(n > 0) {
  if(n % 2 != 0) {
    // calculos
  }
  k++; // para acceder el arreglo a[]
  n = n >> 1; // para acceder al próximo bit
 }
 
Para des-encriptar t,
ejecutamos el mismo proceso
con el número 461 como valor a desencriptar
y los bits de s como valor en n.

Encriptar una cadena, usando el método RSA
p q n Palabra a encriptar
?
Volver.
El problema de la mochila con Programación dinámica.
Teoría: Estructuras. Temas de estudio. Menú Ecuación Temporal -> El problema de la mochila
Cualquier Valor se consigue: V[i, j ] = max(V[i-1, j ], V[i-1, j - pesoi] + vi) Llamado 0-1 knapsack porque
los items no se pueden dividir
Peso limite
Número de articulos
Digite Pesos
Digite Valores
?
Volver.
Arbol de Fibonacci para el termino N.
Teoría: Assembler. Temas de estudio.
Menú Datos DQ, La pila, Recursión ->
N-esimo termino Fibonacci
Digite Termino (0->8):
?
Volver.

Métodos para calcular el número de Dispersión.
Teoría: Estructuras. Temas de estudio. Menú Arboles B/B+
y Dispersión

Digite llave:

Número de dispersión:
?

Método de división Método de Midsquare
Digite tamaño del arreglo:
Digite número de bits centrales:


Método de Transformación Método de Plegamiento
Digite la base:
Digite tamaño del arreglo:
Digite el número de bits de cada grupo:

Volver.

Métodos para resolver colisiones.
Teoría: Estructuras. Temas de estudio. Menú
Arboles B/B+ y Dispersión


Tamaño de los arreglos
Enc. separado
Se usa el Método de división
para calcular el número
de dispersión.
Digite un número primo.		 Enc. Lineal
Se usa el Método de división
para calcular el número
de dispersión.
Digite un número primo.		 Doble Hash
Se usa el Método de división
para calcular el número
de dispersión.
Digite un número primo.		 Prueba cuadrática
Se usa el Método de división
para calcular el número
de dispersión.
Digite un número primo.
Por defecto: Por defecto: Por defecto: Por defecto:

LLaves para insertar en los arreglos
Si no las genera aleatoriamente, digite las
llaves separadas por , y sin espacios.
Si necesita insertar una llave adicional
a las que ya insertó, agregue la llave
al final de las que ya digitó, pero
no borre las anteriores.
Número de llaves (Cuantas llaves va a dispersar aleatoriamente):  
LLaves a Ins/Ret 
Nombres: 

Retiro de llaves. Se puede retirar una llave cada vez.
?
Volver.

Programa para insertar/retirar palabras en un Arbol Eneario.
Teoría: Estructuras. Temas de estudio. Arboles Enearios
Se pueden insertar máximo 20 palabras. Digite las palabras
separadas por , y sin espacios. Si necesita insertar una palabra
adicional a las que ya insertó, agregue la palabra al final
de las que ya digitó, pero no borre las anteriores.
?

Distribuidores a nivel Nacional. No a la pirateria. Adquiera un libro.

Teléfonos: 3102563361 (1)4573045
Dirección: Calle 75A No. 20B-41 Bogotá Colombia